Last week we concluded our 3-part introductory series to the zip function. In the third episode we finally answered the question: “what’s the point?” It ultimately led us to the realization that with zip we could unify many wildly different ways of creating instances of types under the umbrella of one single concept. And that allowed us to write code that worked across arrays, optionals, results, validations, lazy values and even async values in an identical manner.

At the end of the episode we provided some exercises to help viewers dive a little deeper into these ideas, and this week we solve most of those problems!

In this series of episodes on zip we have described zipping types as a kind of way to swap the order of nested containers when one of those containers is a tuple, e.g. we can transform a tuple of arrays to an array of tuples ([A], [B]) -> [(A, B)]. There’s a more general concept that aims to flip containers of any type. Implement the following to the best of your ability, and describe in words what they represent:

Exercise 1.1

sequence: ([A?]) -> [A]?

One attempt at implementation this function may to simply discard all nil values from the array, much like what compactMap does. However, why then would we return an optional array [A]?? Seems like that’s not quite the semantics that this function signature is implying.

Maybe instead what we want to do is return an array of non-optional values in the case that all the values are present, and otherwise return nil. This is a nice way to force that every optional value in an array is present:

func sequence<A>(_ xs: [A?]) -> [A]? {
  var result: [A] = []
  for x in xs {
    guard let x else { return nil }
    result.append(x)
  }
  return result
}

Exercise 1.2

sequence: ([Result<A, E>]) -> Result<[A], E>

Here we are trying to transform an array of results into a result of an array. One way would be to just discard all the failures from the array, and bundle all the successful values into its own array. However, much like the previous exercise, why would we return a result value if we have just take all the successful values? The semantics are all wrong again.

Instead, it might be more true to this function’s signature to require all the result values in the array to be successful, in which case bundle them into an array, and otherwise return an array, say the first error. This is straightforward to implement:

func sequence<A, E>(_ results: [Result<A, E>]) -> Result<[A], E> {
  var successValues: [A] = []
  for result in results {
    switch result {
    case let .success(value):
      successValues.append(value)
    case let .failure(error):
      return .failure(error)
    }
  }
  return .success(successValues)
}

Exercise 1.3

sequence: ([Validated<A, E>]) -> Validated<[A], E>

This one seems very similar to the previous exercise, but we can now take advantage of some key characteristics of Validated. Instead of bailing on the first error we come across, we can accumulate all of the errors that we encounter.

This is a bit tricky! We use NonEmpty to guarantee that at least one error exists in any invalid state. It might seem tough to accumulate a NonEmpty array from nothing, but we can use Optional as our nothing and safely wrap and unwrap along the way.

func sequence<A, E>(
  _ results: [Validated<A, E>]
) -> Validated<[A], E> {
  var validValues: [A] = []
  var invalidErrors: NonEmptyArray<E>?
  for result in results {
    switch result {
    case let .valid(value):
      validValues.append(value)
    case let .invalid(errors):
      if invalidErrors == nil {
        invalidErrors = errors
      } else {
        invalidErrors?.append(contentsOf: errors)
      }
    }
  }
  if let invalidErrors = invalidErrors {
    return .invalid(invalidErrors)
  } else {
    return .valid(validValues)
  }
}

This solution requires a bit of a dance to make work in an imperative style.

We can use reduce and zip and shorten things. If we start with the knowledge that sequencing an empty array of validated results should return a valid, empty array, we can pass reduce this initial value and accumulate either an array of results or a non-empty array of errors by zipping each current accumulation with an array of the next value.

func sequence<A, E>(
  _ results: [Validated<A, E>]
) -> Validated<[A], E> {
  results.reduce(.valid([])) { vs, v in
    zip2(vs, v.map { [$0] }).map { $0 + $1 }
  }
}

Exercise 1.4

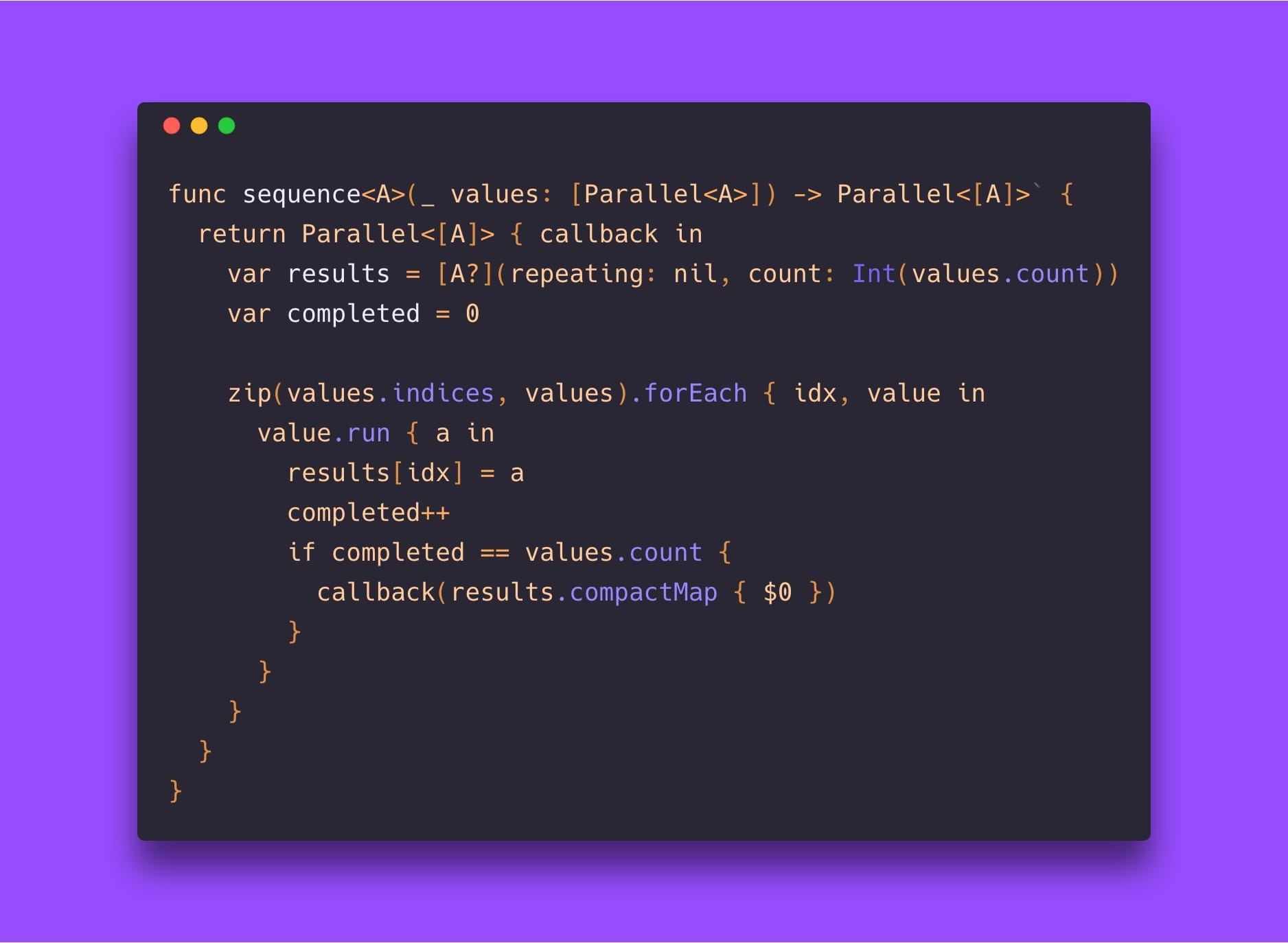
sequence: ([Parallel<A>]) -> Parallel<[A]>

This is a fun one. Here we are trying to transform an array of parallel values into a parallel value of an array. We could try running all of the parallel values in the array concurrently, and then once they are all done collect the values into a single array. One way to accomplish this is to allocate an array the size of the array of parallel values, but filled with nils. Then run all the parallels concurrently, and as they finish stick their values into the allocated array. And when the last one finishes, invoke the callback:

func sequence<A>(_ values: [Parallel<A>]) -> Parallel<[A]> {
  return Parallel<[A]> { callback in
    var results = [A?](repeating: nil, count: Int(values.count))
    var completed = 0

    zip(values.indices, values).forEach { idx, value in
      value.run { a in
        results[idx] = a
        completed++
        if completed == values.count {
          callback(results.compactMap { $0 })
        }
      }
    }
  }
}

Now this implementation has a lot of threading problems, so its not yet production ready. However, a fun bonus exercise might be to find ways to make this thread safe.

Exercise 1.5

sequence: (Result<A?, E>) -> Result<A, E>?

Now we are trying to move the optional ? from inside the result to outside. All we gotta do is reach into the .success case, see if it exists, and if it does, promote it to a non-optional. We’ll also allow errors to pass through:

func sequence<A>(_ result: Result<A?, E>) -> Result<A, E>?` {
  switch result {
  case let .success(value):
    return value.map(Result.success)
  case let .failure(error):
    return .failure(error)
  }
}

Exercise 1.6

sequence: (Validated<A?, E>) -> Validated<A, E>?

This implementation is almost identical to that of Result:

func sequence<A>(_ result: Validated<A?, E>) -> Validated<A, E>?
  switch result {
  case let .valid(value):
    return value.map(Validated.value)
  case let .invalid(error):
    return .invalid(error)
  }
}

Exercise 1.7

Note that all of these functions also represent the flipping of containers, e.g. an array of optionals transforms into an optional array, an array of results transforms into a result of an array, or a validated optional transforms into an optional validation, etc.

Do the implementations of these functions have anything in common, or do they seem mostly distinct from each other?

Looking at all the implementations of sequence above, it is very difficult to find any commonality. Each implementation seems to have used some intimate knowledge of the container types being used. This is in contrast to what we discovered when zipping two nested zippable containers of the same type. In that case we found that we could define zip on the nesting in a very natural way, and it was always the same implementation no matter container type we chose.

And even though there isn’t a single thing in common for all of the implementations, there are some things in common for the implementations having a common “outer” container type, such as array. Can you formalize this relationship?

This is a very powerful idea, and we are only just grasping at it right now. We will have more information on this soon!

Exercise 2

There is a function closely related to zip called apply. It has the following shape: apply: (F<(A) -> B>, F<A>) -> F<B>. Define apply for Array, Optional, Result, Validated, Func, and Parallel.

We can define apply in terms of zip:

func apply<A, B>(_ lhs: [(A) -> B], _ rhs: [A]) -> [B] {
  zip2(lhs, rhs).map { $0($1) }
}

func apply<A, B>(_ lhs: ((A) -> B)?, _ rhs: A?) -> B? {
  zip2(lhs, rhs).map { $0($1) }
}

func apply<A, B, E>(
  _ lhs: Result<(A) -> B, E>, _ rhs: Result<A, E>
) -> Result<B, E> {
  zip2(lhs, rhs).map { $0($1) }
}

func apply<A, B, R>(
  _ lhs: Func<R, (A) -> B>, _ rhs: Func<R, A>
) -> Func<R, B> {
  zip2(lhs, rhs).map { $0($1) }
}

func apply<A, B>(
  _ lhs: Parallel<(A) -> B>, _ rhs: Parallel<A>
) -> Parallel<B> {
  zip2(lhs, rhs).map { $0($1) }
}

Every implementation is exactly the same. The apply function can always be defined in terms of zip and map.

Exercise 3

Another closely related function to zip is called alt, and it has the following shape:

alt: (F<A>, F<A>) -> F<A>

Define alt for Array, Optional, Result, Validated and Parallel. Describe what this function semantically means for each of the types.

This function encapsulates how to combine two values of the same type in some context into just a single context of that type. For arrays, a natural way to do this would be simply array concatenation:

func alt<A>(_ lhs: [A], _ rhs: [A]) -> [A] {
  return lhs + rhs
}

For optionals, let’s write down the signature and see what possible implementations there are:

func alt<A>(_ lhs: A?, _ rhs: A?) -> A? {
  switch (lhs, rhs) {
  case let (.none, .none):
    fatalError()
  case let (.some(lhs), .none):
    fatalError()
  case let (.none, .some(rhs)):
    fatalError()
  case let (.some(lhs), .some(rhs)):
    fatalError()
  }
}

We’ve filled in the first step, which is to simply to switch on the two optionals handed to us. In the first case we have two .none values, and so there’s nothing we could hope to do to return an A value, so we’ll just return nil. In the next 2 cases we have a .some value of type A, and so let’s just return it. The last case is the trickiest, in which we have two .some values of type A. We don’t know anything about A so we can’t combine those values in anyway reasonable way. Therefore we must just decide to return one of them, so we’ll return the first one:

func alt<A>(_ lhs: A?, _ rhs: A?) -> A? {
  switch (lhs, rhs) {
  case let (.none, .none):
    return nil
  case let (.some(lhs), .none):
    return lhs
  case let (.none, .some(rhs)):
    return rhs
  case let (.some(lhs), .some(rhs)):
    return lhs
  }
}

This function should seem quite familiar to you. It’s precisely ??, Swift’s nil coalescing operator. This provides important semantic meaning to the alt function, because in the case of optionals it means “return the first non-nil value, otherwise return nil.” This is what allows you to chain many of these functions together to express the idea of getting the first non-nil value from a bunch of optionals.

Next we will consider Result. How can we combine two Result<A, E>‘s into just a single one? Let’s take some inspiration from our comments on Optional above, and think about this semantically. We will define alt on Result to be the operation of returning the first .success value if it exists, and otherwise return the last .failure. Here’s the implementation:

func alt<A, B, E>(
  _ a: Result<A, E>, _ b: Result<B, E>
) -> Result<(A, B), E> {
  switch (a, b) {
  case let (.success(a), _):
    return .success(a)
  case let (.failure, .success(b)):
    return .success(b)
  case let (.failure, .failure(e)):
    return .failure(e)
  }
}

The implementation for alt on Validated is very similar.

Finally, we have the Parallel type. How can we combine two Parallel<A>‘s into just a single one? If we were to run both parallel values at the same time, and then at a later time procure two values of type A from them, there still wouldn’t be anyway to combine both values into one since we know nothing about the type A. Seems like no matter what we have to discard information. Similar to what we’ve done with Result, maybe we should only take the first one that finishes? We can implement that like so:

func alt<A>(
  _ lhs: Parallel<A>, _ rhs: Parallel<A>
) -> Parallel<A> {
  return .init { f in
    var finished = false
    let callback: (A) -> () = {
      guard !finished else { return }
      finished = true
      f($0)
    }
    lhs.run(callback)
    rhs.run(callback)
  }
}

Semantically this means that we are racing both parallels, and just picking the one that is fastest.

And that’s the solutions to the third part of our 3 part introductory series to zip! This is only the beginning of our journey with zip, there is still a lot more to come.

Until next time!